TSパラメータを用いたスピーカの設計

ポイント

TSパラメータとは？

TSパラメータの TS は Thiele Small の略で，1960-70年前後に研究・整理されたスピーカの特性を表す各種パラメータである．基本的なパラメータ（基礎パラメータ）は以下の７つである． そして，以下のパラメータ（ここでは２次的パラメータと呼ぶ）は全て上のパラメータから計算ができる． これらの値と数式から，基礎パラメータを逆算することもできる．例えば $R_{ms}$ は表記されていないことが多いので，そのようなときは $Rms = \frac{1}{Qms} \sqrt{\frac{Mms}{Cms}}$のように $Q_{ms}$ から計算する．

回路シミュレーションによる設計

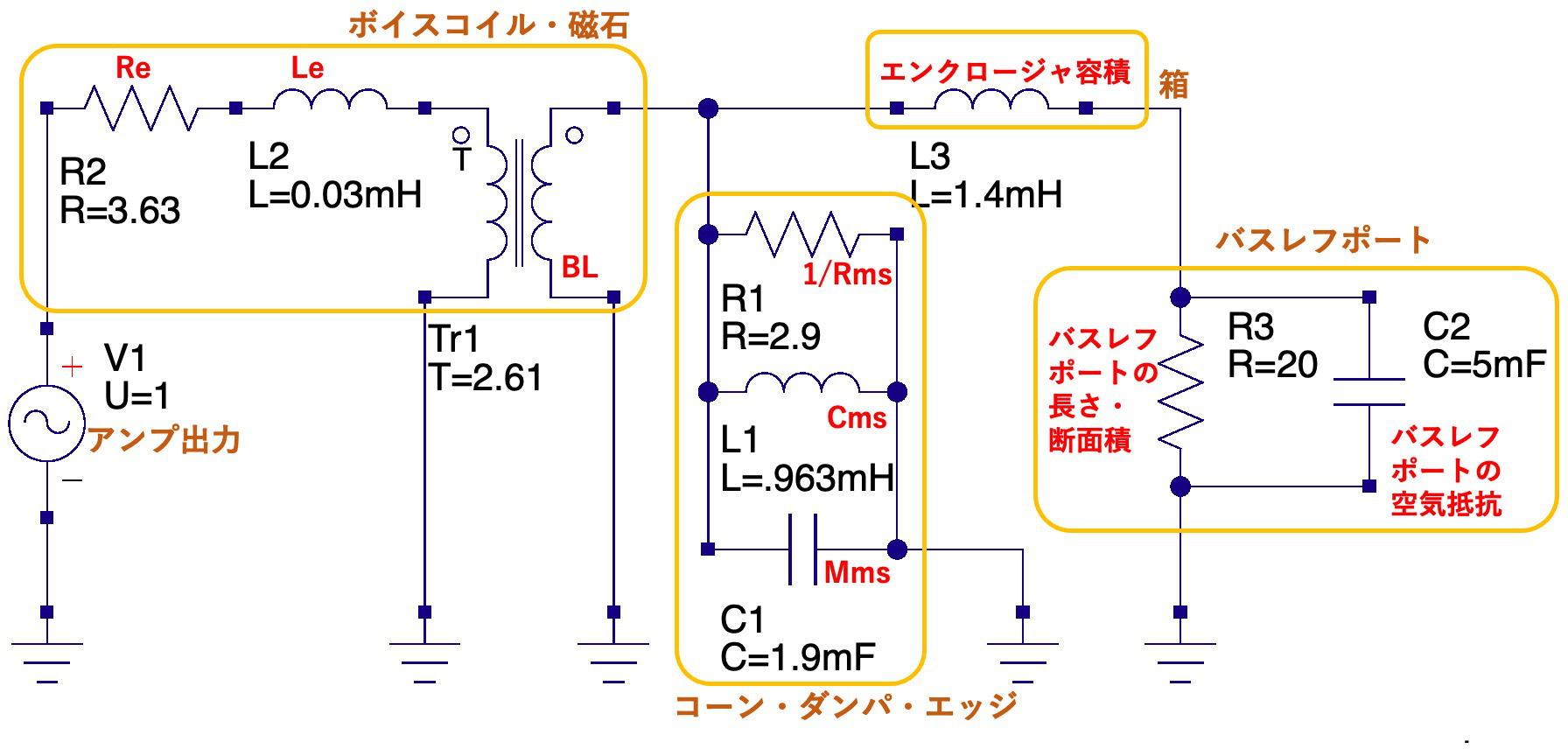
こちらに示しているように，TSパラメータはそのまま電子回路（等価回路）のコイル・コンデンサ・抵抗やトランスの値として設定でき，回路シミュレーションによりスピーカーユニットの特性を調べることができる．さらに，エンクロージャの容積やバスレフポートの特性を等価回路に組み合わせることで，周波数特性などを調べながらスピーカの設計をすることができる．

しかしこの方法には落とし穴がある．それは，スピーカーの過渡的特性である．スピーカーのコーンやエンクロージャが共振しやすいと，残響音により音のクリア感が損なわれる．過渡的特性も回路シミュレーションにより計算できるが，周波数特性ほどぱっと見て分かるようなものではない．そこで次に述べるQ値が用いられる．

Q値に基づく設計

スピーカは各部で共振を起こし，これが不足する低音を補う働きをしたり，不要な残響音で音質を劣化させたりする．低音を補う度合いは周波数特性で調べられるが，残響のしやすさはQ値に基づいて検討することができる．振り子が油のような粘性の高い液体に入っており，重りを動かして手を離したときの動きで例えると，Q が 0.5 より大きい場合は振り子が真ん中を行き過ぎて行ったり来たりする．Qが0.5より小さいと，行き過ぎることなく最終的な位置へ漸近するが，Qが小さすぎると今度は中央へ到達する時間が長くなる．また，周波数特性が最大限フラットになるのは Q = 0.707 であり，これを超えると周波数特性に山ができる．

密閉型の設計

スピーカー単体のQ値は $Q_{ts}$ で与えられている．これをエンクロージャに取り付けると，一般にQ値は高くなる．これは，エンクロージャ内の空気がばねの役割を果たすためである．容積が $V_b$ の密閉型エンクロージャの場合，スピーカのQ値 $Q_b$ は以下の式で表される． $$Q_b = Q_{ts} \sqrt{\frac{V_{as}}{V_b} +1}$$ 例えば$V_b = V_{as}$のとき，エンクロージャによる空気ばねがユニット自身のばねと同じ強さになり，ばねの強さはちょうど倍になる（$C_{ms}$が半分になったのと同じで，上の等価回路で言えば L1 = L3 の状態）．すると，Q値と共振周波数 $F_s$はともに $\sqrt{2}$倍になる．この式の変形により，目的とするQ値を $Q_b$とすると，それを実現するエンクロージャの容積を求めることができる． $$V_b = \frac{V_{as}}{\left( \frac{Q_b}{Q_{ts}} \right) ^2 - 1}$$ この式から分かることは，同じ $Q_b$値を得たいとき，ユニット単体のQ値 $Q_{ts}$が大きいほうが大きなエンクロージャを要求するということである．またこのときの共振周波数は以下の式で与えられる． $$F_b = F_s \frac{Q_b}{Q_{ts}}$$

つまり，共振周波数はQ値の変化率に比例して上昇し，よって $Q_{ts}$の大きなユニットは大きな箱を求める一方で低音再生能力に優れるということが言える．

この式に従い，$Q_b = 0.707, 0.85, 1.0$の３種類に対応する容積をシミュレーションのページでも例に用いたTymphany 社 Peerless PLS-P830985の仕様（$V_{as} = 0.61L, Q_{ts} = 0.63$）を元に求め，周波数特性を求めた．容積は順に 2.35L, 0.74L, 0.40L である．

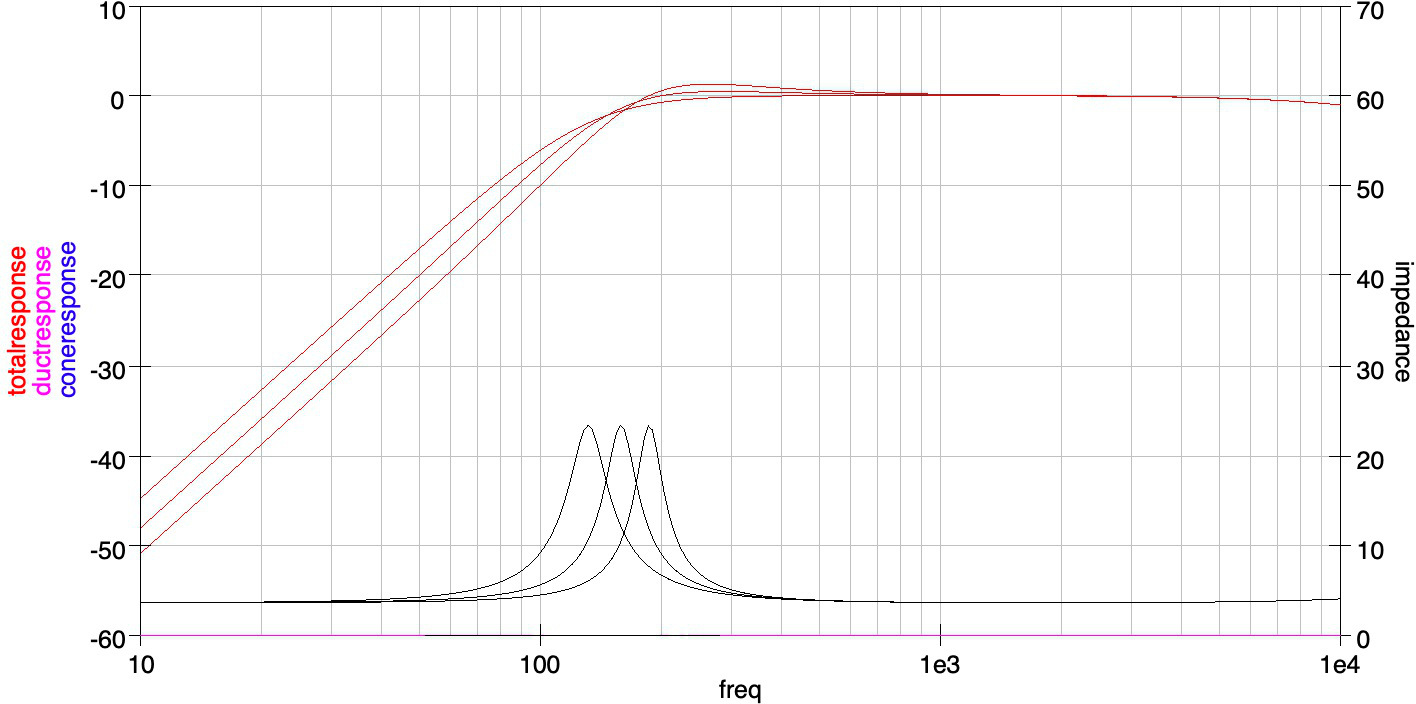
周波数特性の盛り上がり部分もさることながら，やはり目立つのは低域の再生能力の違いであろう．Q値に比例して共振周波数が上がるため，箱を大きめにし，Qを小さくすることで共振周波数を下げることができる．ただし，密閉型エンクロージャでは，いくら容積を大きくしてもQ値をスピーカーユニット単体のQ値よりも低くすることは出来ない（エンクロージャ内部に吸音材を詰めれば少し下げることはできる）．またQ値が上昇するとインピーダンスカーブの幅が狭くなってくることも分かる．

バスレフ型の設計

バスレフ型エンクロージャは２つの共振周波数を持つが，高域側の共振周波数とQ値は通常，同じ容積の密閉型エンクロージャよりもさらに高くなる．また，低域側の共振状態（共振周波数，Ｑ値）はバスレフポートの長さ・太さや空気抵抗により変わる．それら諸々の条件を合わせ，周波数特性がもっともフラットになる特性を得るためには，エンクロージャ容積は以下の式により求めるのが良いと言われている． $$V_b = 20 V_{as} Q_{ts}^{3.3}$$ たしかにこの数式に従ってエンクロージャ容積を求めると良好な結果が得られやすい．下の図は，同じく PLS-P830985の仕様に基づいてエンクロージャ容積（2.66L）を決め，それに合わせて周波数特性が平坦となるようにバスレフポートの仕様を決めた例である．

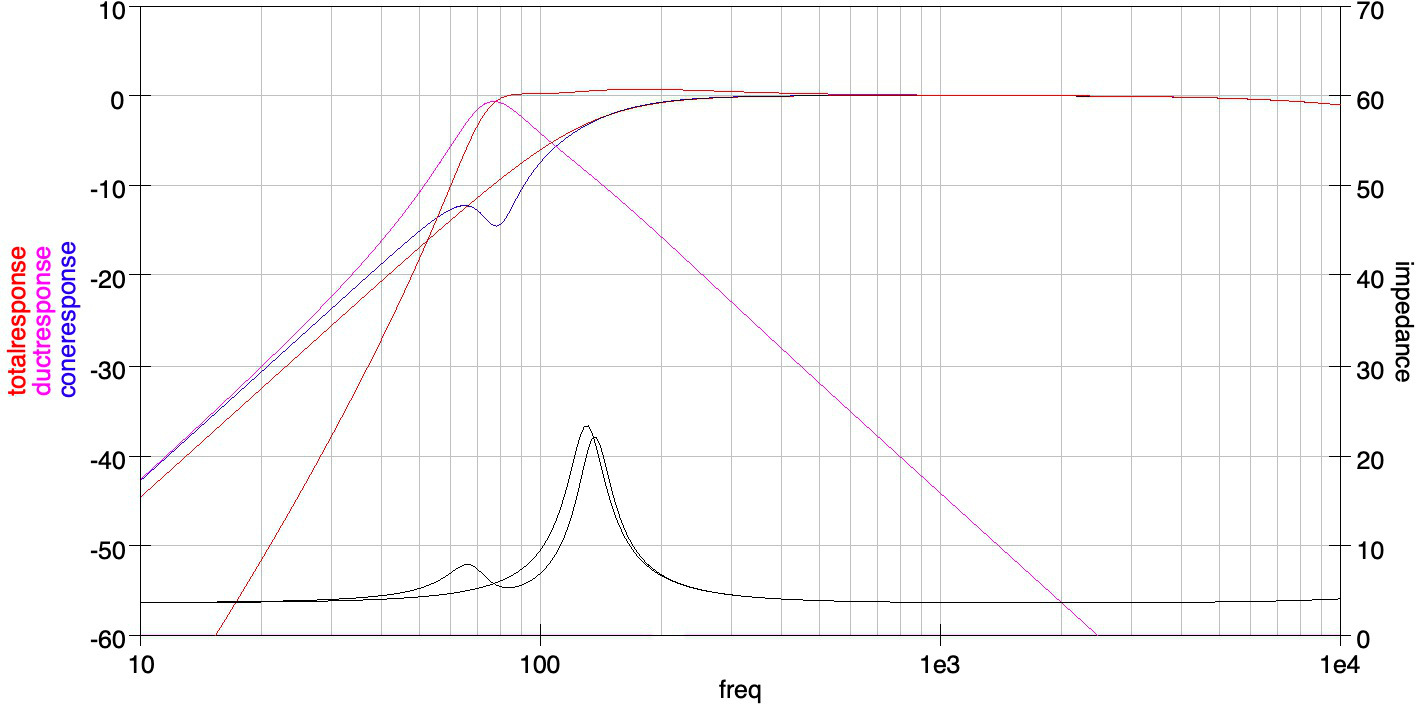
同じ 2.66L の密閉型エンクロージャに取り付けたときの周波数特性と合成しているが，確かに周波数特性の平坦部分は大幅に伸びている．エンクロージャ容積がこの値からずれるに従い，同様のフラットな周波数特性を得るのは難しくなる．

ただし前述のように高域側の共振点のQが上昇していること，低域側はバスレフポートの共振のため非常にQが高いこと（それはコーンからの音圧に比べてバスレフポートからの音圧が最大で５倍程度になっていることからもわかる），などから共振音が低域では支配的になっていることも分かる．密閉型とバスレフ型の周波数特性（２本の赤線）を比べると，ゲインの差は最大でも10dB弱であり（80Hz付近），イコライジングにより十分に補正が可能な範囲である．つまり電気信号的に低音を持ち上げるか，それとも共振現象により機械的にイコライジングをしているかの違いに過ぎない．

Aperiodic 型（音響抵抗型）の設計

aperiodic 型エンクロージャでは，空気抜き部分に空気抵抗を生む綿などを詰めて，コーンの振動を積極的に減衰させる．これにより，密閉型やバスレフ型では困難なQ値の減少が可能となるので，特に小型のエンクロージャを作成するときには役に立つと思われる．しかし，他のパラメータが寸法等から計算できるのに対し，空気抵抗は素材等により変化するのであらかじめ設計でピッタリ良いものを決めてしまうのは難しい．しかし逆に言えば，作ってしまってからの調整の余地が高い．おすすめなのは，綿などの量を変えながらインピーダンスカーブを計測する方法である．

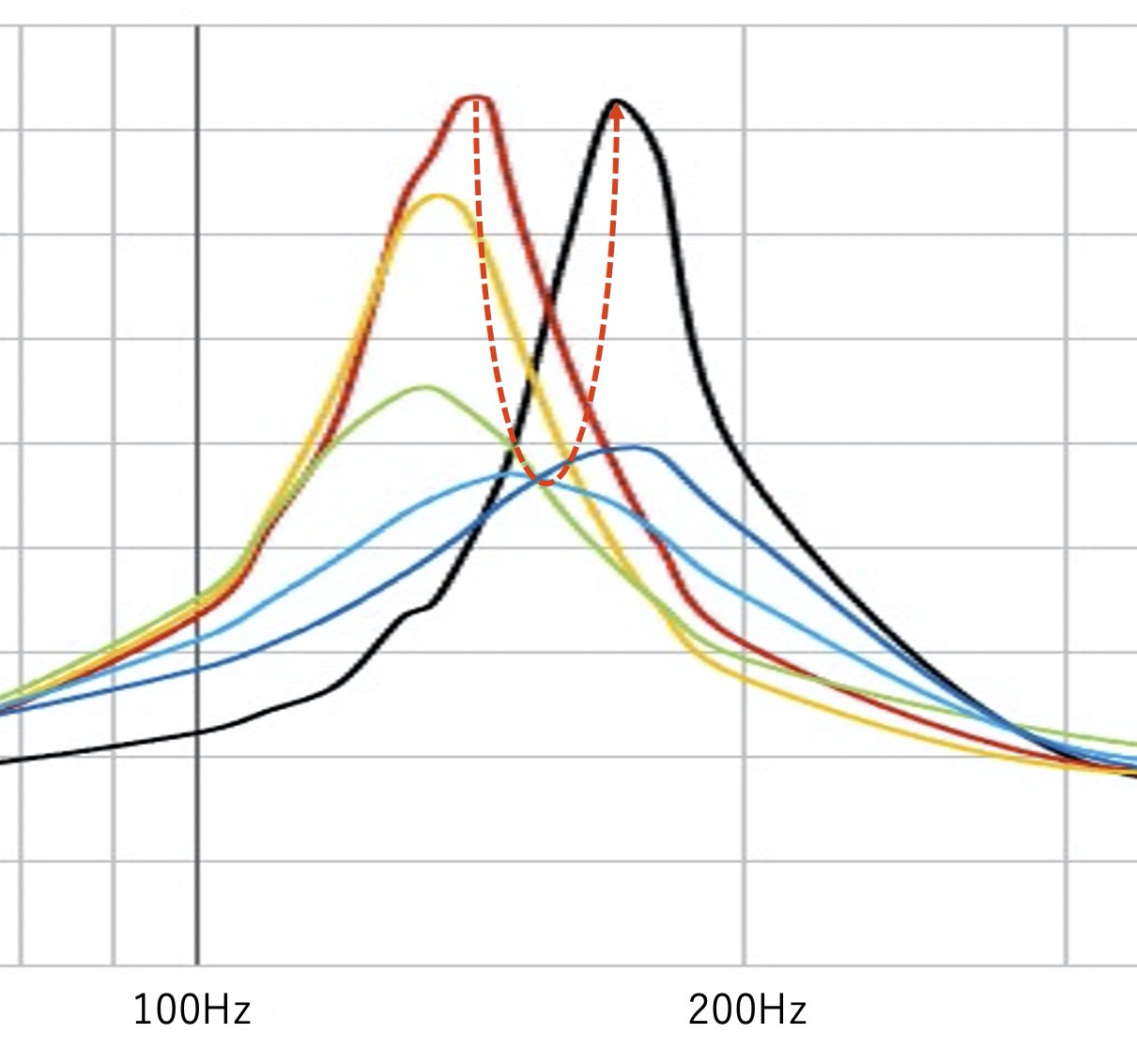
きちんとインピーダンスを計測するには２箇所の交流電圧を正確に測れるよう準備しなくてはならないが，調整のためだけならそれほどの機材は必要ない．アンプとスピーカーの間に抵抗器（1Ω前後）をはさみ，その両端の電圧の変化を様々な周波数で測定する．インピーダンスカーブは，グラフにあるように，出口の開放状態（ほぼ，スピーカー単体の状態に相当）から徐々にピークのインピーダンスが低下しつつピーク位置が高周波にずれていき，再び上昇する．よって，インピーダンスのピークが低くなるように（電圧・電流の変化が小さくなるように）綿の量を調整すればよい．信号発生にはPCのソフト（例えばREW）を使っても良いし，スマホのアプリを使ってもよいだろう．電圧は写真のようにオシロスコープを使ってもよいが，DMM（デジタルマルチメータ）でも計測できると思われる（ただし，周波数が変わったときに電圧が大きく変化しないか要確認．アナログテスターはダイオードの特性から計測が難しい可能性があるが，メーターが触れれば一応は使えるだろう）．

空気抜き穴がバスレフポートのように細く，長さがある構造だと，綿がなくてもバスレフポートと同様に共振性を持つので，空気抜き部分はできるだけ面積が大きく，また，厚みがないほうが良い．厚みがある場合はダンプトバスレフと呼ばれる形式になり，特性は等価回路で調べられるが，Q値を低下させる効果はあまり得られない．