機械式計算機による平方根の計算

機械式計算機は基本的には加減算を行う装置で，これに桁ずらしの機能を加える事によって乗除算を行えるようになっている．さらに単純作業により平方根を求めることも出来る．その原理について解説する．

奇数の減算による平方根の計算

平方根を計算するためには，ある数の２乗が元の数より大きいか小さいかを判断する作業が必要となる．このとき，数の２乗を逐一計算するのは面倒であるため，以下の図のように 1, 3, 5, 7, ... のように奇数を順に引いていく作業を行う．

上の図で分かるように，初項 1 の奇数の数列の和は常に N² である．そこで機械式計算機では，元の数から 1, 3, 5, 7, ... と奇数の数列を順に引いていき，負になる直前の値をもとの数の平方根とする．余った数はより下位の桁の計算で必要となるが，これについては後で述べる．

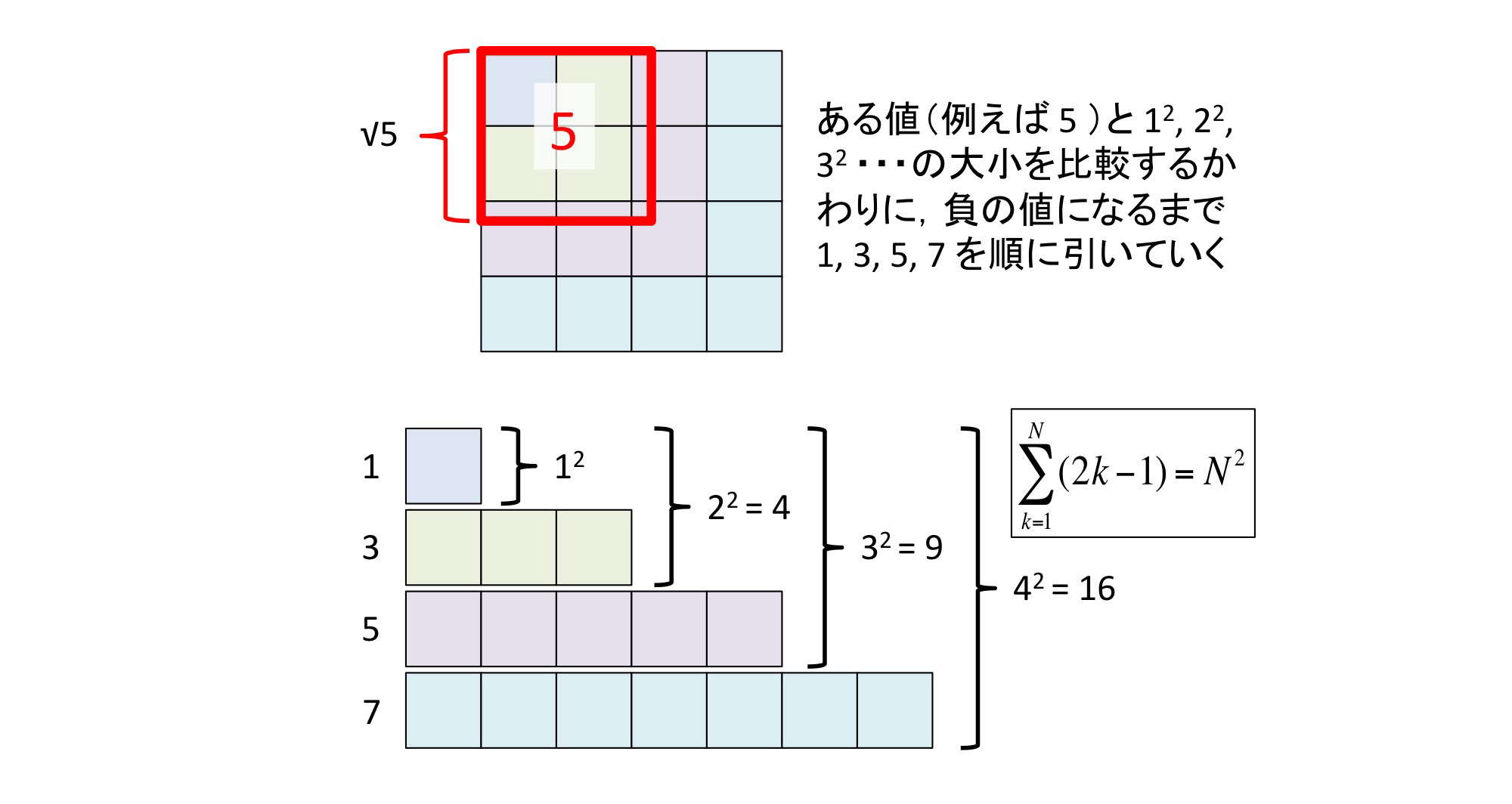
上位桁の確定値と奇数の減算による開平

ここでは 5 の平方根を求めることとし，その手順について説明する．

まず初期状態として平方根を求めたい数 5 をおく．次に，１回目として 1 を減じて差 4 を得る．次にこの 4 から ３ を減じ，1 を得る．さらに 1 から 5 を減じると負の数となるので，2 < √5 < 3 であり，√5 は 2.??? という数になることが分かる．

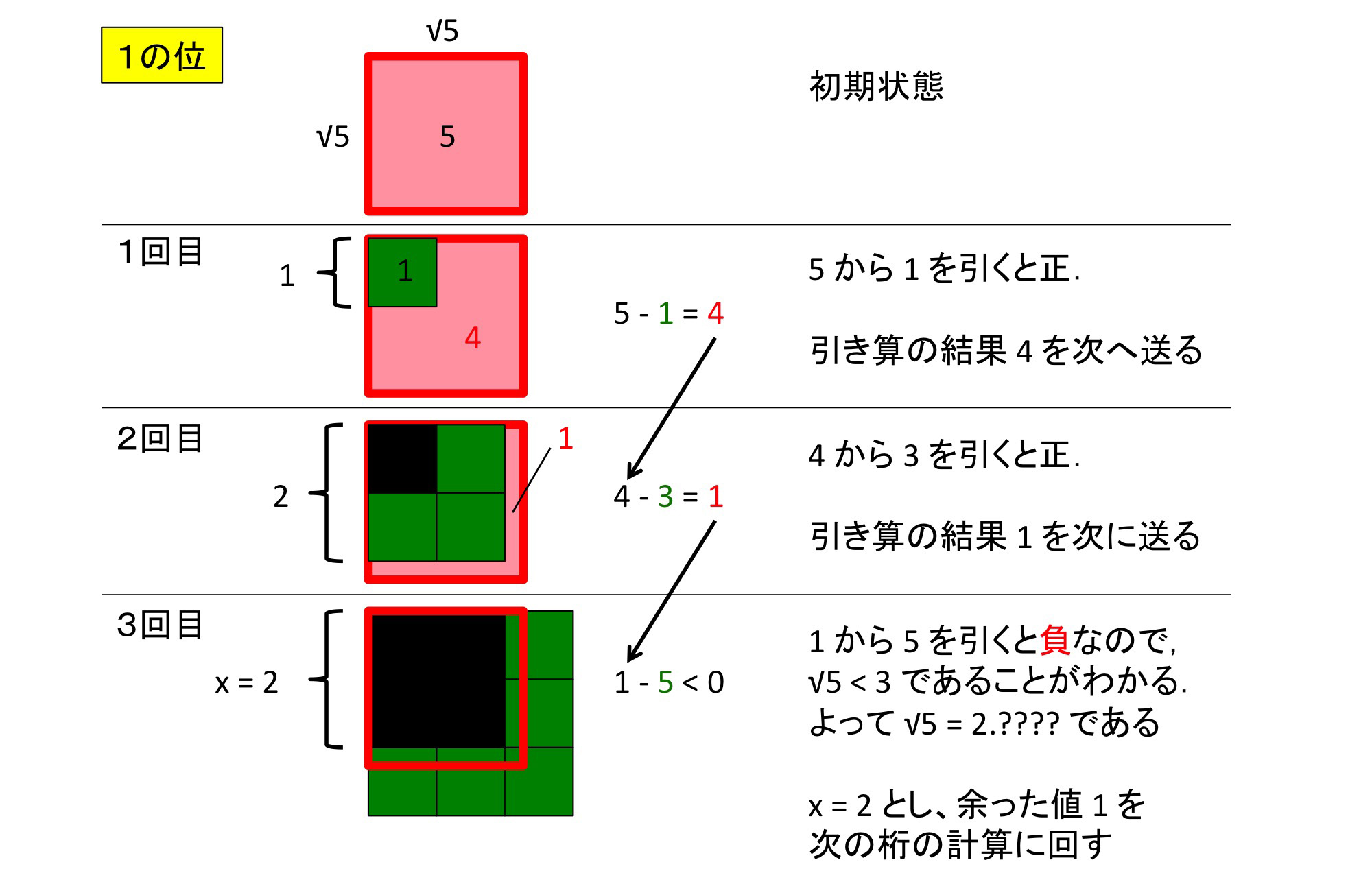
次に，残った値 1 を用いてより下位の桁の値を求めていく．

x + 0.1 の２乗について考えると，これは (x + 0.1)² = x² + 2x・0.1 + 0.1² のように展開できる．最初の項 x² は既に引き去ってあるため，残りの値と 2x・0.1 + 0.1² の大小関係を調べることになる．上の図では 2x・0.1 の領域が青色の長方形（２つ）に，また 0.1² の領域が緑色の正方形に相当する．そこでこれまでに求められた１の位の平方根の値 x を一桁右にずらして（1/10倍して）から２倍し，それに 0.01 を加えた値を残りの値から減じる．√5 の場合は，0.41 を引いて残りが 0.59 となる．２回目は 0.01 の正方形の数が３個になり，３回目は５個になる．これは１の位の計算と同様に， 1, 3, 5, 7, ... という値を減じる操作となる．この２回目の引き算も成功し，次の３回目で負の値となる．よって小数点以下第１桁の値が 2 であることが確定し，√5 は 2.2??? という値となることが分かる．引き算の残り 0.16 と，確定部分の平方根の値 2.2 を次の小数点以下第２桁の計算に用いる．

上の図では見やすさのため，0.01 の厚みを大きく書いている（実際にはもっと薄い領域となるはずである）．ここでも 0.1 の位と同様に，青の長方形領域が２つと，緑の正方形が１つ現れる．青の長方形領域は，長い方の辺の長さが確定部分の平方根の値（2.2）であり，それに 0.01 をかけたものを２つ引くことになる．また正方形領域は，この桁でも同様に引き算の回数に応じて 1, 3, 5, 7, ... と増えていく．４回目の減算で負の値となるため，2.23 < √5 < 2.24 となり，√5 は 2.23??? という値となることが決まる．この手順を繰り返していくと，いくらでも高精度な平方根の計算が可能となる．

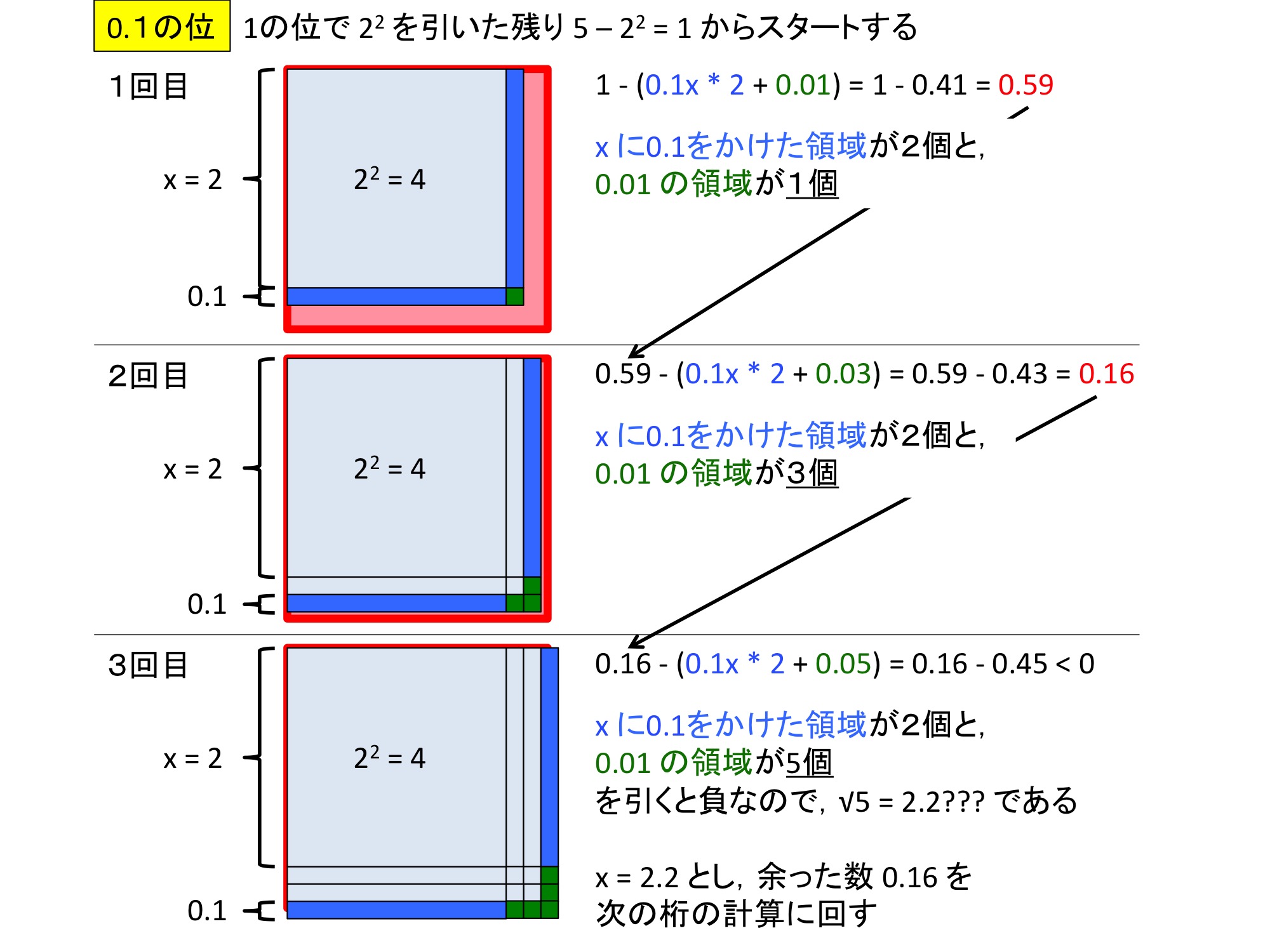
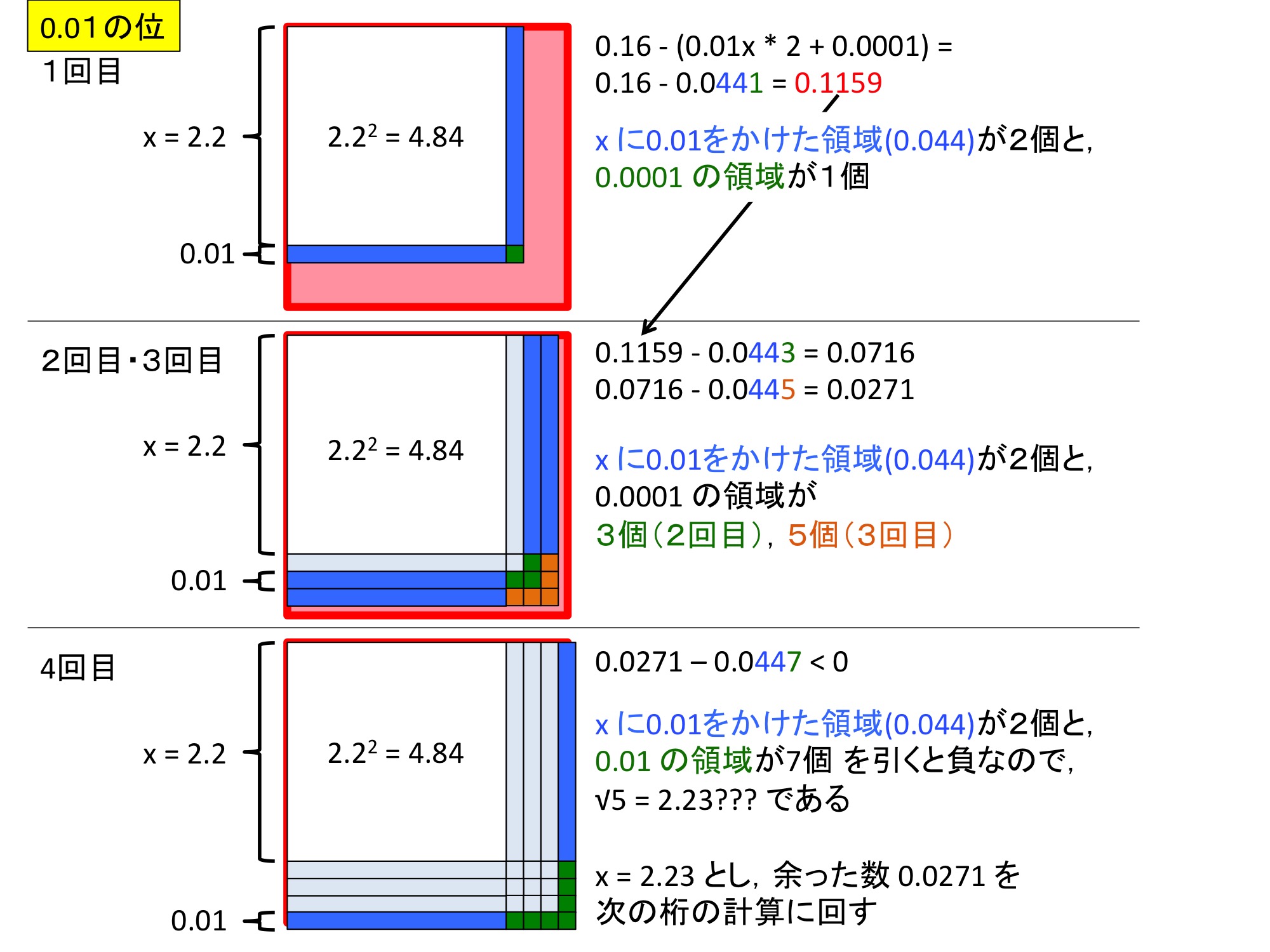
平方根計算の実例

√5 の計算をタイガー計算器とクルタ計算機で実行する様子の動画を以下に示す．

まず最上位桁に 5 を加算し，加算回数のカウンタ（左のカウンタ）をリセットする．次に，その桁で 1, 3, 5 と引いていくと，5を引いた時にベルが鳴る．タイガー計算機では繰り下がりにより 0 未満になった時（または加算により最大値を超えて一周した時）にベルが鳴るため，ベルを聞くとすぐにノブを逆回転（加算方向）に回し，最後の引き算をなかったことにする．最後に引いた数は，引き算に成功した回数の２倍より 1 だけ多い（1, 3 の引き算に成功し，5 の引き算で負の値になったときは，2 回の引き算に成功している）ので，最後の桁を１つ戻す操作を行う．先の説明では上位桁の確定値を x として下位の桁の計算に用いたが，「青色の長方形」は必ず２個現れるので，機械式計算機による平方根の計算では 2x の値を作りながら計算を進めていくのである．つまり，手前左のカウンタには平方根の値が上位から確定していくが，それと同時に右奥の減算値の表示には，平方根の値の２倍が上位桁から現れてくることになる．

ある桁の計算が完了したら１桁送る．この操作により，平方根の確定値（の２倍）に 0.1, 0.01, ... を順にかけていくことになる．そしてその確定値の最終桁の次の桁が，上の説明における「緑の正方形」に相当する桁となるため，その桁の値を 1, 3, 5, ... と増やしながらさらに計算を続行する．1, 3, 5, 7, 9 と５回引いて，さらにまだ引ける時はその桁を 1 まで戻し，１つ上の桁に 1 を加える．これは，11, 13, 15, 17, 19 を順に引いていくことに相当する．

このタイガー計算機では √5 = 2.236067977 と１０桁までを計算することが出来る．

クルタ計算機では，ノブを引き上げた状態（赤い線が見えている状態）で減算，押し込んだ状態で加算となり，ノブの回転方向は一定である．まず最上位桁に５をセットし，減算回数のカウンタをリセットしておくのはタイガー計算器の例と同じである．ノブを引き上げた状態で引いていき，上位桁に繰り下がりが生じた時はノブを押し込んで同じ値を加算することで元に戻す．その桁の減算値ノブを１段戻し，１桁ずらしてから，次の桁を 1, 3, 5, 7, ... と変えながら引いていく手順はタイガー計算器による平方根の計算と全く同じである．クルタ計算機では引き算の回数を減算していくのか加算していくのかを切り替えるノブが背面にあり，これを減算に合わせておくことを忘れないようにする．

このクルタ計算機は桁数が多い方の機種（Type II) であるので，√5 = 2.2360679 と８桁までを計算することが出来る．